Логические выражения
Логическое выражение — это утверждение или комбинация утверждений, которые могут быть истинными (true) или ложными (false).
Примеры логических выражений:
- x > y (x больше, чем y)
- a == b (a равно b)
- (x > 5) && (y < 10) (x больше 5 и y меньше 10)
- (a != b) || (c == d) (a не равно b или c равно d)
Логические выражения могут быть использованы в различных языках программирования, таких как Java, Python, C++ и других. Они играют важную роль в управлении потоком выполнения программы и помогают программистам создавать более гибкие и мощные программы.
Логические операции
Логические операции — это операции, которые выполняются над логическими выражениями и результатом их выполнения является новое логическое выражение.
В программировании, логические операции обычно выполняются над булевыми значениями (true/false).
Примеры логических операций:
- Операция «И» (AND), конъюнкция: обозначается символом && или * или ∧, возвращает true только если оба операнда равны true. Например, «сходить в магазин И купить молоко» — будет выполнено только если оба условия верны.
- Операция «ИЛИ» (OR), дизъюнкция: обозначается символом || или + или ∨, возвращает true, если хотя бы один из операндов равен true. Например, «если завтра будет солнечно ИЛИ я не буду занят — я поеду на пикник» — здесь выполнение произойдет если хотя бы одно из условий верно.
- Операция «НЕ» (NOT), отрицание: обозначается символом ! или ¬, инвертирует логическое значение операнда (true становится false, и наоборот). Например, «не пойду в кино» — значение станет true, если изначально мы планировали пойти в кино, а после применения NOT мы получим отрицание этого утверждения — что мы не пойдем.
- Тождественное равенство — это логическая операция, которая используется для проверки равенства двух логических выражений во всех возможных случаях. Она обозначается как «≡» или как «==» в некоторых языках программирования. Результат тождественного равенства является логическим значением истинности (true) или ложности (false). Например, выражение «x = y ≡ y > x» вернет значение false.
- Импликация (следование) — это логическая операция, которая определяет, как одно логическое выражение влияет на другое. Она обозначается как «→» или как «->» в некоторых языках программирования. Импликация говорит о том, что если одно выражение (предпосылка) является истинным, то другое выражение (заключение) также является истинным. Если же предпосылка ложна, то заключение может быть как истинным, так и ложным. Например, выражение «если я поеду в отпуск, то я возьму с собой книги» может быть записано как «поездка в отпуск → взятие книг». Если я поеду в отпуск, то я обязательно возьму с собой книги. Но если я не поеду в отпуск, то я могу взять книги или не брать их в зависимости от других факторов.
Примеры логических операций в повседневной жизни:
- «Если сегодня пятница И я не занят, то я поеду на вечеринку». Здесь операция «И» используется для определения условий, при которых мы поедем на вечеринку.
- «Если я буду дома ИЛИ будет идти дождь, то я останусь дома». Здесь операция «ИЛИ» используется для определения условий, при которых мы останемся дома.
- «Я НЕ буду есть мясо, потому что я вегетарианец». Здесь операция «НЕ» используется для инвертирования утверждения о том, что мы будем есть мясо.
Таблица истинности логических выражений
Таблица истинности — это таблица, которая показывает все возможные значения истинности логического выражения в зависимости от значений его логических компонентов (переменных). В таблице истинности для каждого возможного набора значений переменных указывается, является ли исходное логическое выражение истинным или ложным.
Обычно, в такой таблице, вместо логических значений False и True (Ложь и Истина), используются значения 0 (False) и 1 (True).
Рассмотрим пример таблицы истинности для простого выражения из одной логической операции — операции отрицания (NOT). Пусть дана переменная x, которая может принимать значения true или false. Тогда таблица истинности для операции отрицания выглядит следующим образом:
| x | NOT x |
|---|---|
| 0 | 1 |
| 1 | 0 |
Как видно из таблицы, если x равно true (1), то NOT x будет равно false (0), а если x равно false (0), то NOT x будет равно true (1).
Теперь рассмотрим пример более сложного логического выражения, которое включает в себя несколько логических операций. Пусть даны две переменные x и y, которые могут принимать значения true или false. Рассмотрим логическое выражение «x AND (NOT y)». Таблица истинности для этого выражения будет выглядеть следующим образом:
| x | y | NOT y | x AND (NOT y) |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
Как видно из таблицы, выражение «x AND (NOT y)» будет истинным только в том случае, если x равно true, а y равно false. Если хотя бы одна из переменных равна false, то исходное выражение будет ложным.
Таблицы истинности для конъюнкции, дизъюнкции, импликации
Конъюнкция, дизъюнкция и импликация — это три основные бинарные логические операции. Бинарные логические операции работают с двумя логическими выражениями (условиями) и возвращают результат в виде одного логического значения — истинности или ложности.
Таблицы истинности для этих операций выглядят следующим образом:
Конъюнкция (AND)
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
В таблице истинности для конъюнкции, результат будет истинным только в том случае, если оба условия истинны.
Дизъюнкция (OR)
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
В таблице истинности для дизъюнкции, результат будет истинным, если хотя бы одно из условий истинно.
Импликация (IF-THEN)
| A | B | A → B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
В таблице истинности для импликации, если условие A истинно, то результат будет истинным только в том случае, если условие B тоже истинно. Если же условие A ложно, то результат всегда будет истинным, независимо от того, что является условием B.
Приоритет логических операций
Приоритет логических операций — это порядок, в котором операции выполняются в логическом выражении.
Если в выражении присутствуют несколько операций, то порядок их выполнения зависит от приоритета операций.
В общем случае, порядок выполнения операций в выражении определяется следующими правилами:
- Сначала выполняются операции в скобках.
- Затем выполняются операции логического отрицания (NOT).
- Затем выполняются операции логического умножения (AND).
- Затем выполняются операции логического сложения (OR).
- В конце выполняются операции импликации (IF-THEN) и эквивалентности (IF AND ONLY IF).
Таким образом, операции в логическом выражении выполняются в порядке убывания приоритета.
Например, в выражении «A OR B AND C» операция AND выполнится первой, так как у нее приоритет выше, чем у операции OR. Однако, если требуется изменить порядок выполнения операций, можно использовать скобки, например: «(A OR B) AND C». В этом случае, операция OR выполнится первой, а затем результат будет умножен на C, так как операция AND имеет более высокий приоритет, чем операция OR.
Важно помнить, что правильный порядок выполнения операций в выражении может значительно влиять на его результат, поэтому при работе с логическими выражениями важно следить за приоритетом операций и правильно использовать скобки.
Построение таблиц истинности логических выражений с помощью Python
Чтобы построить таблицу истинности логического выражения, нам понадобятся знания и навыки из урока по циклам в Python.
Если вы не разбирали данный урок, то обязательно начните прямо сейчас! И лишь после этого, возвращайтесь к изучению данного материала.
Особенное внимание уделите таким темам как:
Построение таблицы истинности для конъюнкции трех условий.
Для построения таблицы истинности для конъюнкции трех условий можно воспользоваться языком программирования Python и его возможностью работы с логическими операциями.
Для создания всех возможных комбинаций 0 и 1 (истинных и ложных значений), воспользуемся тройным вложенным циклом for Каждый цикл перебирает два возможных значения (0 и 1) для каждого из операндов: x, y, z
Для этого можно написать следующий код:
# выводим заголовок таблицы
print("a | b | c | a ∧ b ∧ c")
print("--|---|---|---------")
# перебираем все возможные значения переменных a, b и c
for a in range(2):
for b in range(2):
for c in range(2):
# вычисляем значение выражения и выводим результат в таблицу
result = a and b and c
print(f"{int(a)} | {int(b)} | {int(c)} | {int(result)}")
В данном коде мы задаем начальные значения переменных a, b и c как False. Затем мы выводим заголовок таблицы истинности и перебираем все возможные значения переменных a, b и c, используя вложенные циклы. Для каждой комбинации значений переменных мы вычисляем значение выражения и выводим результат в таблицу. В конце каждой строки таблицы мы переходим на новую строку с помощью команды `print()`.
Результатом выполнения данного кода будет таблица истинности для конъюнкции трех условий:
a | b | c | a ∧ b ∧ c
--|---|---|---------
0 | 0 | 0 | 0
0 | 0 | 1 | 0
0 | 1 | 0 | 0
0 | 1 | 1 | 0
1 | 0 | 0 | 0
1 | 0 | 1 | 0
1 | 1 | 0 | 0
1 | 1 | 1 | 1
Как можно видеть из таблицы, значение конъюнкции трех условий будет равно 1 (True) только в том случае, когда все три условия истинны. В остальных случаях, значение выражения будет равно 0 (False).
Решение основано на принципах работы с булевыми значениями (True/False) и логическими операциями (and). При помощи циклов for и операторов range мы перебираем все возможные комбинации значений переменных a, b и c, и для каждой комбинации вычисляем значение выражения a ∧ b ∧ c. Результаты вычислений выводим в таблицу истинности с помощью команды print().
Построение таблицы истинности для импликации в Python
Как обозначается импликация в Python?
Как мы ранее узнали, импликация — это логическая операция, которая означает «если…, то…». В Python, импликацию можно реализовать двумя способами:
- Надежный, но длинный. Через предобразование:
A → B == not A or B - Быстрый но ненадежный. Можно напутать с приоритетами операций, когда есть скобки.
A → B== A<=B
Давайте построим таблицу истинности для импликации с помощью Python:
def implication(a, b):
return (not a) or b
print("Таблица истинности для импликации:")
print("a | b | a -> b")
print("-"*13)
for a in [True, False]:
for b in [True, False]:
result = implication(a, b)
print(int(a), "|", int(b), "|", int(result))
Здесь мы определяем функцию implication, которая принимает два аргумента a и b и возвращает значение импликации a -> b. Затем мы выводим заголовок таблицы истинности и используем два вложенных цикла `for`, чтобы перебрать все возможные комбинации значений a и b. Для каждой комбинации мы вычисляем результат функции `implication` и выводим значения a, b и результат в виде строки таблицы.
Результат выполнения программы будет следующим:
Таблица истинности для импликации:
a | b | a -> b
-------------
1 | 1 | 1
1 | 0 | 0
0 | 1 | 1
0 | 0 | 1
Здесь 1 означает True, а 0 — False. Как видим, значение импликации a -> b истинно только в тех случаях, когда a ложно или a и b истинны одновременно.
Решение заданий ЕГЭ с помощью Python
Типовое задание:
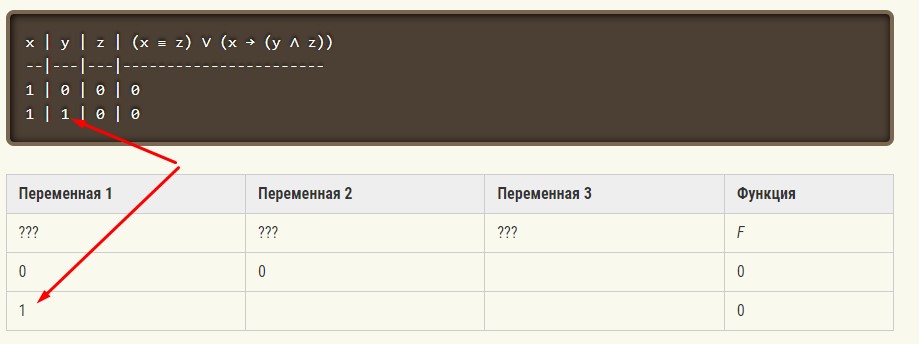
Логическая функция F задаётся выражением (x ≡ z ) ∨ (x → (y ∧ z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| ??? | ??? | ??? | F |
| 0 | 0 | 0 | |
| 1 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение
Для построения таблицы истинности данного логического выражения можно воспользоваться языком программирования Python и его возможностью работы с логическими операциями. Для этого можно написать следующий код:
# выводим заголовок таблицы
print("x | y | z | (x ≡ z) ∨ (x → (y ∧ z))")
print("--|---|---|-----------------------")
# перебираем все возможные значения переменных x, y и z
for x in range(2):
for y in range(2):
for z in range(2):
# вычисляем значение выражения и выводим результат в таблицу
result = (x == z) or (not x or (y and z))
#Фильтруем таблицу, печатаем только те значения, где результат = 0 (False)
if not result:
print(f"{x} | {y} | {z} | {int(result)}")
В данном коде мы задаем начальные значения переменных x, y и z как False. Затем мы выводим заголовок таблицы истинности и перебираем все возможные значения переменных x, y и z, используя вложенные циклы. Для каждой комбинации значений переменных мы вычисляем значение выражения и выводим результат в таблицу. В конце каждой строки таблицы мы переходим на новую строку с помощью команды print().
Результатом выполнения данного кода будет таблица истинности для данного логического выражения:
x | y | z | (x ≡ z) ∨ (x → (y ∧ z))
--|---|---|-----------------------
1 | 0 | 0 | 0
1 | 1 | 0 | 0Как можно видеть из таблицы, значение данного логического выражения будет равно 1 (True) только в тех случаях, когда x и z равны, или когда x равно True, а y и z также равны True. В остальных случаях, значение выражения будет равно 0 (False).
Фильтруем таблицу истинности
Для анализа таблицы, нам нужны только те значения итогового выражения, которые принимают значение 0 (False), потому что в задании, для расшифровки, приведен фрагмент только с ложными значениями выражения.
Для этого, внутри переборной конструкции из трех циклов for, сначала вычисляется значение логического выражения, а потом добавлено условие:
if not result:
print(f"{x} | {y} | {z} | {int(result)}")В случае, если итоговое выражение (переменная result), имеет ложное значение, мы печатаем фрагмент таблицы истинности.
Сопоставляем получившийся фрагмент из программы и задания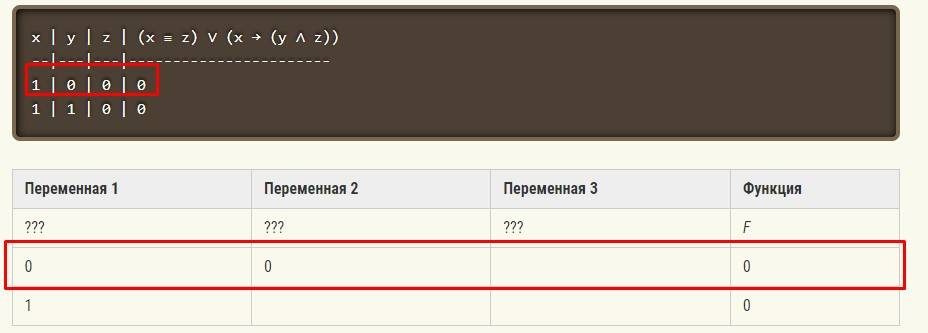
Шаг 1. Сравниваем две таблицы: получившуюся с помощью программы и фрагмента, данного в задании.
Сравнивая две таблицы, мы видим только одну строку, где две исходных переменных одновременно равны 0 (False). Только значение переменной3 пусто. Значит, можно сделать вывод, что переменная3 — это x.
Шаг 2. Оставшаяся строка фрагмента из задания, содержит только одно значение — 1 (Переменная1).
Ей соответствует нижняя строка результатов программы. Переменную x, мы исключаем, так как нашли ее на шаге 1. Значит — переменная 1 — это y, так как именно у нее значение 1 (True). Оставшаяся переменная 2 соответствует переменной z.
Ответ: yzx
Построение таблицы истинности с помощью Excel
Для построения таблицы истинности в Excel мы можем использовать логические функции И(AND) и ИЛИ (OR). Давайте создадим новую таблицу в Excel и заполним ее значениями:
| A | B |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
Здесь столбцы A и B содержат все возможные комбинации значений True и False. Теперь мы можем добавить два новых столбца C и D, чтобы вычислить значения конъюнкции и дизъюнкции соответственно.
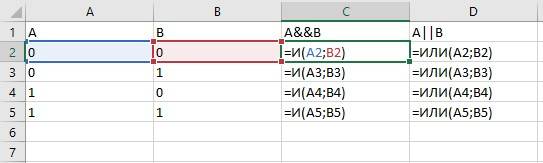
Для конъюнкции мы можем использовать функцию И. В ячейку C2 введите формулу =И(A2;B2) и скопируйте эту формулу в ячейки C3:C5. Результаты вычислений должны быть такими:
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
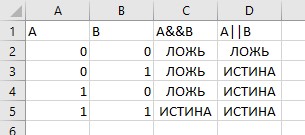
Для дизъюнкции мы можем использовать функцию ИЛИ. В ячейку D2 введите формулу =ИЛИ(A2;B2) и скопируйте эту формулу в ячейки D3:D5. Результаты вычислений должны быть такими:
| A | B | C | D |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Здесь мы видим, что результат дизъюнкции ИЛИ равен True только в тех случаях, когда хотя бы один из аргументов равен True. Результат конъюнкции И равен True только в том случае, когда оба аргумента равны True.
Реализация импликации и тождества в Excel
Для построения таблицы истинности для импликации в Excel мы можем использовать логическую функцию ЕСЛИ. Давайте создадим новую таблицу в Excel и заполним ее значениями:
| A | B |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
Здесь столбцы A и B содержат все возможные комбинации значений True и False. Теперь мы можем добавить новый столбец C, чтобы вычислить значения импликации.
Для импликации мы можем использовать функцию ЕСЛИ, которая возвращает True, если условие истинно, и False, если условие ложно. В ячейку C2 введите формулу =ЕСЛИ(A2=1;B2;1), где ; используется вместо запятой в русской локали Excel. Скопируйте эту формулу в ячейки C3:C5. Результаты вычислений должны быть такими:
| A | B | C |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Здесь мы видим, что результат импликации равен True только в тех случаях, когда логическое условие А истинно и логическое условие B также истинно, или когда логическое условие А ложно. Для выражения «A → B» это означает, что если A истинно, то B также должно быть истинно, но если A ложно, то B может быть истинно или ложно.
Для реализации тождества с помощью Excel, можно использовать формулу: =ЕСЛИ(A2=B2;1;0).
Решение задания 2 ЕГЭ с помощью Excel
Задание.
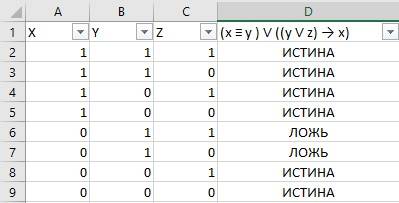
Логическая функция F задаётся выражением (x ≡ y ) ∨ ((y ∨ z) → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| ??? | ??? | ??? | F |
| 1 | 1 | 0 | |
| 1 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 1 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение.
Для построения таблицы истинности в Excel нам нужно создать столбцы для каждой переменной и один столбец для всего выражения. Затем мы используем функции Excel для вычисления значений выражения для всех возможных комбинаций значений переменных.
- Создайте столбцы для переменных x, y и z.
- Добавьте еще один столбец, который будет содержать выражение (x ≡ y ) ∨ ((y ∨ z) → x).
- В первой строке столбцов переменных напишите заголовки «x», «y» и «z».
- Заполните каждый столбец переменной всеми возможными комбинациями значений 0 и 1. Например, для двух переменных (x и y) у нас будет 4 строки: 1 и 1, 1 и 0, 0 и 1, и 0 и 0.
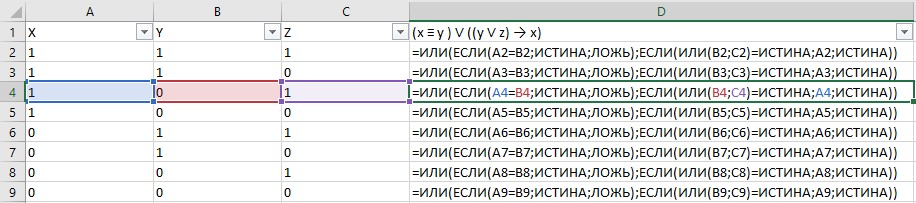
- Для столбца, содержащего выражение, используйте следующую формулу для первой строки и скопируйте ее для всех остальных строк:
=ИЛИ(ЕСЛИ(A2=B2;ИСТИНА;ЛОЖЬ);ЕСЛИ(ИЛИ(B2;C2)=ИСТИНА;A2;ИСТИНА))
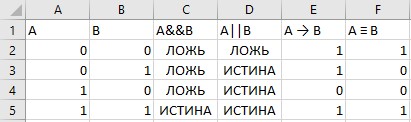
После того, как вы скопировали формулу для всех строк, вы должны увидеть таблицу, которая выглядит примерно так:
Здесь мы видим результат вычисления выражения для каждой возможной комбинации значений переменных.
Затем, мы должны отфильтровать результат и вывести только ложные значения выражения.
И сопоставляем с фрагментом задания
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| ??? | ??? | ??? | F |
| 1 | 1 | 0 | |
| 1 | 0 |
Мы видим, что у Переменной 3 оба значения равны ИСТИНА. Это соответствует переменной y.
Переменная x у нас всегда принимает ложные значения. Значит Переменная 2 точно не x. Переменная 2 — это z.
Оставшаяся Переменная 1 соответствует x.
Ответ: xzy
Индивидуальное и групповое обучение «ЕГЭ»
Если вы хотите сдать ЕГЭ на высокий балл, могу помочь. Запишитесь на мой курс «ЕГЭ» и начните свой путь в мир ИТ уже сегодня!
Контакты
Для получения дополнительной информации и записи на курсы свяжитесь со мной:
Телеграм: https://t.me/Vvkomlev
Email: victor.komlev@mail.ru
Объясняю сложное простыми словами. Даже если вы никогда не работали с ИТ и далеки от программирования, теперь у вас точно все получится! Проверено десятками примеров моих учеников.
Гибкий график обучения. Я предлагаю занятия в мини-группах и индивидуально, что позволяет каждому заниматься в удобном темпе. Вы можете совмещать обучение с работой или учебой.
Практическая направленность. 80%: практики, 20% теории. У меня множество авторских заданий, которые фокусируются на практике. Вы не просто изучаете теорию, а сразу применяете знания в реальных проектах и задачах.
Разнообразие учебных материалов: Теория представлена в виде текстовых уроков с примерами и видео, что делает обучение максимально эффективным и удобным.
Понимаю, что обучение информационным технологиям может быть сложным, особенно для новичков. Моя цель – сделать этот процесс максимально простым и увлекательным. У меня персонализированный подход к каждому ученику. Максимальный фокус внимания на ваши потребности и уровень подготовки.